曹行宇的Blog
0%

JErasure库的相关介绍

发表于 更新于 分类于 Valine：

JErasure库提供一般的RS码和CRS码两种编码方式，是基于C的纠删码的类库。

一、Galois Field

（一）基本概念

1.1.1 域（field）

域代表一组元素和元素间的四则运算的集合。其中，域内元素的四则运算必须满足封闭性，也就是说域内元素进行四则运算后得到的结果仍为域内元素。

1.1.2 有限域（finite field）

有限域即为仅含有有限个元素的域。有限域又称作伽罗华域(Galois Field)。记为\(GF\)。例如，\(GF(7)\)的元素为0~6.

有限域中必须含有加法单位元和乘法单位元。加法单位元即域中的零元，即存在元素\(e\)，使得域中任一元素\(a\)，有\(e+a = a\)。乘法单位元即域中的幺元，即存在元素e，使得域中任一元素\(a\)，有\(e*a = a\)。\(GF(p)\)的加法单位元和乘法单位元分别为0和1.

此外，有限域中的每个元素还应有对应的逆元。乘法逆元与我们常见的倒数类似。即存在元素b，使得\(b*a = e\)，则\(b\)为\(a\)的乘法逆元。其中\(e\)为乘法单位元。加法逆元与我们常见的相反数类似。即存在元素\(b\)，使得\(b+a = e\)，则\(b\)为\(a\)的加法逆元。其中\(e\)为加法单位元。

有限域中的减法和除法即为加法和乘法的逆过程。\(GF(p)\)的加法和乘法与实数域内的加法和乘法相似，只不过最后要模\(p\)。即\(GF(a+b) = (a+b) \mod p， GF(a×b) = (a×b) \mod p\)。

一般而言，\(p\)应为质数，因为如果\(p\)非质数，则可能有一些元素找不到乘法逆元。例如\(GF(9)\)中，元素3找不到\(GF(9)\)中的一个元素\(a\)使\(3\times a \mod p = 1\)，即3没有乘法逆元。

（二）\(GF(2^w)\)

1.2.1 \(GF(2^w)\)

\(GF(2^w)\)上的加法运算和乘法运算不使用一般的加法和乘法，而是使用多项式的计算。

1.2.2 多项式计算

\(GF(2^w)\)上的多项式计算中，多项式的系数为1或0，即只能取\(GF(2)\)上的元素；当进行加法运算时，合并同类项时，不是一般的系数相加，而是进行异或计算，且加法和减法的操作一致。例如： \[ (x^3+x^2)+(x^4+x^2)=x^4+x^3 \]

\(GF(2^w)\)上的多项式的最高次不超过\(w\)。例如，在\(GF(2^3)\)中，\(f_1(x)=x^2+1\)为\(GF(2^3)\)的多项式，\(f_2(x)=x^3+x^2+1\)则不是\(GF(2^3)\)的多项式。

但是，多项式的加法计算后的结果一定仍为域中多项式，而对于多项式乘法，若直接按一般的多项式乘法计算的计算结果则可能不再是域中的多项式。与\(GF(p)\)类似，需要找到一个多项式对其取模，使之仍然为域中多项式。因此，提出本原多项式的概念。

1.2.3 本原多项式/质多项式(\(\text{primitive polynomial}\))

质多项式与质数的概念类似，质多项式即为不能表示成除幺元对应的多项式与该多项式以外的其他多项式的乘积，即不能再进行因式分解的多项式。例如，在\(GF(2^4)\)中，\(f(x) = x^4 + 1\)不是\(GF(2^4)\)上的质多项式，因为\(f(x) = (x^2 + 1) × (x^2 + 1)\)。\(g(x) = x^4 + x + 1\)是\(GF(2^4)\)上的质多项式，因为它不可再分解。

以\(GF(2^3)\)为例，指数小于3的多项式一共有8个，分别是\(0，1，x，x+1，x^2，x^2+1，x^2+x，x^2+x+1\)，一共有8个多项式。其对应的系数分别可以表示为000，001，010，011，100，101，110，111，若用十进制表示，则正好为0，1，2，3，4，5，6，7。这说明0~7与8个多项式之间有着必然的映射关系，每个多项式会对应一个值。对于\(GF(2^3)\)，取素多项式\(f(x) = x^3+x+1\)，则\(x+1\)的乘法逆元为\(x^2+x\)，因为\(((x+1) × (x^2+x) mod (x^3+x+1) = 1)\)，也就是说即使\(\mod 8\)不能构成一个有限域，但是由质多项式仍然可以为域中每个元素找到一个乘法逆元。 此时，多项式的乘法即可得到解决。例如，在\(GF(2^3)\)内： \[ x\times (x^2+1)=x\times (x^2+1)\mod (x^3+x+1)=(x^3+x)\mod (x^3+x+1)=1 \]

对于多项式除法，根据\[r(x) = q(x)t(x) + s(x)\]，其中\(r(x),q(x),t(x),s(x)\)均为\(GF(2^w)\)上的多项式，\(q(x)\)表示\(GF(2^w)\)上的质多项式。易知\(r(x) \mod q(x) = s(x)\)，且显然有\(dim\ s(x) < dim\ q(x)\)。（\(dim\ f(x)\)表示的是\(f(x)\)的最高次的次数）。

根据上述理论，即可根据质多项式来得到\(GF(2^w)\)的所有元素。\(GF(2^w)\)中元素的生成过程如下：

1
2
3
1. 给定一个初始集合{0, 1, x};
2. 将这个集合的最后一个元素乘以x。如果得到的结果的度(dim) ≥ w，则将结果 mod q(x)，将结果加入集合中;
3. 重复2，直到集合中有2^w个元素。此时最后的一个元素乘以x再 mod q(x)的值必定为1.

举个栗子： \(w = 2\)时，\(q(x) = x^2 + x + 1\)，初始集合为\(\{0, 1, x\}\)，

最后一个元素为\(x\)，乘以\(x\)后为\(x^2\)，\(dim\ (x^2) = 2\)，因此要对\(q(x)\)取模，得\((x^2) \mod (x^2 + x + 1) = x + 1\)；此时集合更新为\(\{0, 1, x, x+1\}\)；

再将最后一个元素乘以\(x\)，为\(x^2 + x\),仍需要对\(q(x)\)取模，得\((x^2 + x) mod (x^2 + x + 1) = 1\),结束上述过程。即\(GF(2^2) = \{0, 1, x, x+1\}\)。

也就是说，只需要找到对应\(GF(2^w)\)上的本原多项式\(q(x)\)即可通过\(x\)代换得到\(GF(2^w)\)，即： \[ GF(2^w) = GF(2)[x]/q(x) \]

常用的本原多项式有：

w = 4:   x^4 + x + 1
w = 8:   x^8 + x^4 + x^3 + x^2 + 1
w = 16:  x^16 + x^12 + x^3 + x + 1
w = 32:  x^32 + x^22 + x^2 + x + 1
w = 64:  x^64 + x^4 + x^3 + x + 1

例如，\(GF(2^4)\)的元素生成：(\(P(x) = x^4 + x + 1\)) GF(2^4)的元素生成过程

由上述计算结果，可以构建以下两个表（正表和反表)：

i 0 1 2 3 4
gflog[i] - 0 1 4 2
gfilog[i] 1 2 4 8 3
5 6 7 8 9 10
8 5 10 3 14 9
6 12 11 5 19 7
11 12 13 14 15
7 6 13 11 12
14 15 13 9 -

其中，gflog[i]表（反表）是将二进制映射成多项式，例如将5映射成多项式，即\(gflog[5] = 8\),即\(x^8 = 5\)；gfilog[i]表（正表）是将多项式映射成二进制(值),例如将5(即\(x^5\))映射成值，即\(gfilog[5] = 6\),即\(x^5 = 6\).

对于乘法和除法，可以由如下方式进行： \[ x^a\times x^b=x^{a+b};\\ x^a/x^b=x^{a-b}. \]

因此，我们在计算可以\(a×b\)时，可以先得到\(a = x^m, b = x^n\); 则\(a\times b = x^{m + n}, a/b = x^{m - n}\).

即：先将\(a，b\)查找反表（gflog[i]）得到\(m，n\)；计算\(m + n\)或者\(m - n\)，然后基于结果查找正表（gfilog[i]）得到乘法和除法的结果。需要注意的是，在计算\(m + n\)和\(m - n\)时，若结果大于等于15或小于0，则需要对15(\(2^w - 1\))取模。因为0是单独存在的，在\(GF(2^w)\)中没有哪个元素的任意次方等于0.

再举个栗子：

7 × 9 = gfilog[gflog[7] + gflog[9]] = gfilog[10 + 14] = gfilog[9] = 10

(\(7 × 9 = x^{10} × x^{14} = x^{10 + 14} = x^{24 \mod 15} = x^9 = 10\))

13 / 11 = gfilog[gflog[13] - gflog[11]] = gfilog[13 - 7] = gfilog[6] = 12

(\(13 / 11 = x^{13} / x^7 = x^{13-7} = x^6 = 12\))

因此，构造正反表之后，可以大大简化乘法和除法的计算，可以直接通过加法和查表得到结果，而不需要再进行繁琐的取模等运算。

二、CRS码

（一）RS码简介

介绍CRS码之前先要弄明白RS码是什么。RS码就是Reed-Solomon码，是一种MDS码。编码时将k个数据块通过一定方式编码成m个校验块，我一般把它写成RS(k, m)，最多可以容忍m个数据块失效。解码时通过m个幸存块来恢复所有的数据块。那么RS码是通过什么方式来编码和解码的呢？ RS码通过构造生成矩阵来编码数据块。前k×k为单位阵，后m×k为生成矩阵。编码过程即为生成矩阵与数据块进行矩阵的乘法，即得到k个数据块和m个校验块。 Encoding 当有不多于m个块失效时，为了恢复数据块，则取出k个幸存块对应的生成矩阵的行构成一个矩阵，对该矩阵的逆与对应的幸存块相乘即可恢复出数据块。 例如，数据块\(D_2，D_3\)和校验块\(P_1\)丢失，取出k个幸存块对应的生成矩阵的行，例如取出\(D_1，D_4， ...，D_k，P_2，P_3\)，一共\(k\)个数据块，有： Decoding_1 再将左边的子矩阵的逆乘到右侧，即有： Decoding_2 此时，所有的数据块就被恢复出来了。再要恢复校验块，很简单，再进行一次编码操作即可得到所有正确的校验块了。 然后问题来了，RS码的编解码步骤已经清楚了，现在就只有一个待解决的问题了，那就是得找到一个合适的生成矩阵，使得该生成矩阵的任意k行都线性无关，也就是说任意k行组成的矩阵的行列式不为0，此时即可保证任意k行组成的子矩阵必定可逆。因此，在RS码中，我们一般采用 范德蒙德矩阵（Vandermonde Matrix） 作为生成矩阵，此时该矩阵的任意k行组成的子矩阵一定可逆。 用范德蒙德矩阵进行编码的时间复杂度为O(mk)，解码的时间复杂度为O(k^3)。 在利用范德蒙德矩阵编码的时候，我们可以采用对数/反对数表的方法将乘法运算转换成加法运算，并且在迦罗华域中，加法运算转换成了XOR运算。 显然，这种方法要比直接复制副本存储的空间开销小得多，但是解码时花费的时间有点多了。所以，基于Reed-Solomon码，又有另一种纠删码被提出 -- Cauchy Reed-Solomon Code。

（二）CRS Code简介

2.2.1 Cauchy Matrix

Cauchy矩阵是由两个交集为空的集合构成的矩阵。具体为：

令C = [cij]m\(\times\)n，有集合X = {\(x_1, x_2, \cdots, x_m\)}，Y = {\(y_1, y_2, \cdots, y_n\)}，且X∩Y = ∅。矩阵C中的元素\(c_{ij}\)满足 \[ c_{ij} = \frac{1}{x_i + y_j} \] 则矩阵C为Cauchy矩阵。

Cauchy矩阵有一个很重要的性质，即Cauchy矩阵的任意一个子方阵必定可逆。且求逆的时间复杂度为O(\(n^2\))，\(n\)为子方阵的维数。 例如，对于\(X = \{1, 2\}\)，\(Y = \{0, 3, 4, 5, 6\}\)，其编解码过程如下： Cauchy matrix‘s encoding and decoding 从编解码过程来看，柯西编解码最大的运算量是乘法和加法运算。柯西编解码为了降低乘法复杂度，采用了有限域上的元素都可以使用二进制矩阵表示的原理，将乘法运算和加法运算转换成了迦罗华域“与运算”和“XOR逻辑运算”，提高了编解码效率。

从数学的角度来看，在迦罗华有限域中，任何一个GF(\(2^w\))域上的元素都可以映射到GF(2)二进制域，并且采用一个二进制矩阵的方式表示GF（\(2^w\)）中的元素。例如，GF（\(2^3\)）域中的元素可以表示成GF（2）域中的二进制矩阵： GF(2^3) to GF(2) 其中，\(M(e)\)的第\(i\)列为\(V(e * 2^{i-1})\).其中\(e*2^{i-1}\)为\(GF(2^3)\)上的乘法。通过以上规则，可以得到： \[ M(e_1) * V(e_2) = V(e_1e_2)，\\ M(e_1) * M(e_2) = M(e_1e_2) \\ \] . 举个栗子：

GF(2^3)的乘法转化为GF(2)的乘法 根据上述理论，将Cauchy matrix的每个元素(\(e\))全部替换成\(M(e)\)，以此替换即可将计算从\(GF(2^w)\)上的计算变为\(GF(2)\)的计算(位运算)。为了可以使两矩阵能进行乘法计算，将每个数据块并没有划分为\(2^w\)大小，而是划分为\(w\)，即将每个数据块分为\(w\)块。例如，对前文所述的Cauchy matrix和\(GF(2^3)\)，有： convert Cauchy matrix to bitmatrix ### 2.2.2 相关证明 上述结论可以证明。证明过程如下：

令\(P(x)\)为\(GF(2)[x]\)中的\(L\)次本原多项式。由前文介绍的Galois Field中的理论，可以得知\(GF(2^L)\)中的元素可以由\(f(x) = \sum_{i = 0}^{L-1}f_ix^i\)表出，其中\(f_i\in GF(2)\)。记列向量\[(f_1, f_2, \cdots, f_{L-1})\]为\(f(x)\)的系数向量（coefficient vector）。

对属于\(GF(2^L)\)的任意多项式\(f(x)\)，令\(\tau(f)\)为系数向量的矩阵，其中\(\tau(f)\)的第\(i\)列为\[x^{i-1}f(x) \pmod {P(x)}\]的系数向量。 根据以上定义，有以下引理：

（1）\(\tau(0)\)是零矩阵；

（2）\(\tau(1)\)是单位矩阵；

（3）\(\tau\)是单射；

（4）\(\tau(f) + \tau(g) = \tau(f+g)\)；\(f\)和\(g\)是\(GF(2^L)\)的多项式；

（5）\(\tau(f)\tau(g) = \tau(fg)\)；\(f\)和\(g\)是\(GF(2^L)\)的多项式

其中(1)到(3)很容易证明，这里只证明(4)和(5): \[ x^i(f+g) = x^if + x^ig \pmod {P(x)} \] 其中\(x^i(f + g)\)表示以\(\tau(f + g)\)的第\(i\)列为系数的多项式，\(x^if\)和\(x^ig\)表示以\(\tau(f)\)和\(\tau(g)\)的第\(i\)列为系数的多项式。显然，(4)得证。 令\(f^{(i)}\)表示\(\tau(f)\)的第\(i\)列; 令\(\{g_0^{(j)}, g_1^{(j)}, \cdots, g_{L-1}^{(j)}\}^T\)为\(\tau(g)\)的第\(j\)列。则有： \[ \sum_{i=0}^{L-1}g_i^{(j)}x^i = x^{j-1}g \mod p(x) \] (其中\(p(x)\)为\(GF(2^L)\)上的质多项式，\(g = g_0^{(1)}+g_1^{(1)}x + g_2^{(1)}x^2 + \cdots + g_{L-1}^{(1)}x^{L-1}\))

因\(\tau(f)\tau(g)\)的第\(j\)列为： \[ \begin{bmatrix} f^{(1)} & f^{(2)} & \cdots & f^{(L)} \end{bmatrix} \begin{bmatrix} \cdots & g_0^{(j)} & \cdots \\ \cdots & g_1^{(j)} & \cdots \\ \vdots & \vdots & \vdots \\ \cdots & g_{L-1}^{(j)} & \cdots \\ \end{bmatrix} \] \[ \begin{aligned} &= g_0^{(j)}f^{(1)}+g_1^{(j)}f^{(2)}+ \cdots +g_{L-1}^{(j)}f^{(L)}\\ &= \sum_{i=0}^{L-1}g_i^{(j)}f^{(i+1)} \end{aligned} \]

这就是下面这个的多项式的系数向量： \[ \sum_{i=0}^{L-1}g_i^{(j)}(x^if) = f\sum_{i=0}^{L-1}g_i^{(j)}x^i = x^{j-1}fg \mod p(x) \] 即：\(\tau(f)\tau(g)\)的第j列与\(\tau(fg)\)的第j列相同

即：\(\tau(f)\tau(g)=\tau(fg)\)

也就是说，将\(GF(2^w)\)映射成\(\tau(GF(2^w))\)后，仍然有加法和乘法的不变性，即: \[ M(e_1) * M(e_2) = M(e_1e_2) \]

若将\(M(e_2)\)的第一列提取出来，即为： \[ M(e_1) * V(e_2) = V(e_1e_2) \]

至此，前面的理论已完全证毕。

现在再来证明Cauchy matrix的求逆过程可以在\(O(n^2)\)的时间复杂度内完成。

对于Cauchy矩阵的任意一个子方阵\(C = [c_{ij}]_{n\times n}\): \[ \begin{bmatrix} \frac{1}{x_1+y_1} & \frac{1}{x_1+y_2} & \cdots & \frac{1}{x_1+y_n} \\[10pt] \frac{1}{x_2+y_1} & \frac{1}{x_2+y_2} & \cdots & \frac{1}{x_2+y_n} \\[10pt] \vdots & \vdots & \ddots & \vdots \\[10pt] \frac{1}{x_n+y_1} & \frac{1}{x_n+y_2} & \cdots & \frac{1}{x_n+y_n} \end{bmatrix} \] 其行列式 \[ \det C = \frac{\prod_{i<j}(x_i-x_j)\prod_{i<j}(y_i-y_j)}{\prod_{i,j = 1}^n(x_i+y_j)} \] 令\(C^{-1} = [d_{ij}]\)，则有

\[ d_{ij} = (-1)^{i+j}\frac{\det C_{ji}}{\det C_j} \] 其中\(c_{ji}\)表示删除了第\(j\)行和第\(i\)列的矩阵\(C\)。令 \[ \begin{align} a_k &= \prod_{i<k}(x_i-x_k)\prod_{k<j}(x_k-x_j)\\ b_k &= \prod_{i<k}(y_i-y_k)\prod_{k<j}(y_j-y_k)\\ c_k &= \prod_{i=1}^n(x_k+y_i)\\ f_k &= \prod_{i=1}^n(y_k+x_i) \end{align} \] 因此，有：

\[ \begin{align} \det C &= \frac{\prod_{k=1}^na_kb_k}{\prod_{k=1}^ne_kf_k}\\ \det C_{ji} &= \frac{\det C e_jf_i}{a_jb_i(x_j+y_i)} \end{align} \] 因此：

\[ d_{ij} = (-1)^{i+j}\frac{e_jf_i}{a_jb_i(x_j+y_i)} \] 所以\(4n\)个未知量\(a_k, b_k, c_k, f_k\)可以在\(O(n^2)\)的时间复杂度内被解出，而\(d_{ij}\)则可由上述公式在\(O(1)\)的时间复杂度得到，因此，Cauchy矩阵的求逆过程可以在\(O(n^2)\)的时间复杂度内得到。

三、JErasure库源码分析

（一）Galois.c/Galois.h

这两个文件中定义的函数比较简单。首先：

1
2
3
4
5
6
7
8
9
10
static int prim_poly[33]; //对应的w的各个质多项式

static int mult_type[33]; //对于不同的w采用不同的乘法计算

static int nw[33];		  //存放的是2^w的值，nwm1是2^w-1的值，即GF(2^w)的最大值

static int *galois_log_tables[33];  //各个w(1~30)的反表
static int *galois_ilog_tables[33]; //各个w(1~30)的正表
static int *galois_mult_tables[33]; //各个w(1~30)的乘法表
static int *galois_div_tables[33];  //各个w(1~30)的除法表

以上是Galois.c中定义的一系列表，这些表将会在之后进行构造。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
int galois_create_log_tables(int w)
//创建w的正反表，且将正表复制了两份，以便构建乘法表和除法表，然后将正表的初始位置(galois_log_tables[w][0]置为第二个副本的起始位置)，返回0表示构建成功，返回1表示失败

int galois_logtable_multiply(int x, int y, int w)
//查正反表计算x*y

int galois_logtable_divide(int x, int y, int w)
//查正反表计算x/y

int galois_create_mult_tables(int w)
//构建大小为nw[w] * nw[w]的乘法表和除法表

int galois_ilog(int value, int w)
//求value对应的二进制的值，即x^value对应的数值

int galois_log(int value, int w)
//求value对应的多项式，即value对应的x^i的i值

int galois_shift_multiply(int x, int y, int w)
//移位乘法，不需要任何表即可实现，但需要w次乘2，w次判断。
//对于x*y，先计算出y*2, y*2^2, y*2^3, ..., y*2^w-1的值，然后将x化为二进制，对x的第i位为1的，取出y*2^i进行异或得到结果。

int galois_multtable_multiply(int x, int y, int w)
//查乘法表求x*y

void galois_invert_binary_matrix(int *mat, int *inv, int rows)
//用初等变换法计算二进制矩阵mat的逆矩阵，mat的每一个元素表示一行，应为w，即w = row，若不可逆则停止运行程序

int galois_inverse(int x, int w)
//若w = 23~32，用移位，否则直接用galois_single_multiply计算1/x

int galois_shift_inverse(int x, int w)
//以移位的方式求y的倒数
//先由y得到mat2[w] = {y, y*2, y*2^2, ..., y*2^w-1}，通过galois_invert_binary_matrix函数得到mat2[w]的逆矩阵inv，inv[0]即为1/y的值

int galois_single_multiply(int a, int b, int w)
//计算x*y，对于不同的w采用不同的乘法策略：
/********************************
 * w = 1~9: 构造乘法表，查乘法表
 * w = 10~22: 构建正反表，查正反表
 * w = 23~31: 用移位乘法
 * w = 32: 用裂乘
 ********************************/

int galois_single_divide(int a, int b, int w)
//计算a/b，对于不同的w采用不同的除法策略：
/********************************
 * w = 1~9: 构造除法表，查除法表
 * w = 10~22: 构建正反表，查正反表
 * w = 23~32: 先得到b的倒数(galois_inverse(b, w))，再用galois_single_multiply函数计算(分为w = 23~31和w = 32的两种策略)
 ********************************/

int galois_shift_divide(int x, int y, int w)
//利用galois_shift_inverse函数得到b的倒数，再利用移位乘法得到a/b的值

int galois_multtable_divide(int x, int y, int w)
//查除法表得x/y

int galois_create_split_w8_tables()
//创建裂乘表

int galois_split_w8_multiply(int x, int y)
//裂乘

其中，裂乘的思路如下： 对于\(x\times y\)，以\(GF(2^{32})\)为例，\(x\)和\(y\)均为域内元素，则\(x\)和\(y\)可表示成： \[ x = x_0+2^8\times x_1+2^{2\times 8}\times x_2+2^{3\times 8}\times x_3 \\ y = y_0+2^8\times y_1+2^{2\times 8}\times y_2+2^{3\times 8}\times y_3 \]

其中\(x_i\)和\(y_i\)均为unit8_t型数据，\(i \in \{0, 1, 2, 3\}\). 则： \[ \begin{aligned} x\times y &= ( x_0+2^8\times x_1+2^{2\times 8}\times x_2+2^{3\times 8}\times x_3)\times (y_0+2^8\times y_1+2^{2\times 8}\times y_2+2^{3\times 8}\times y_3)\\ &=x_0y_0\\ &+\ 2^8\times (x_0y_1+x_1y_0)\\ &+\ 2^{2 \times 8}\times (x_0y_2+x_1y_1+x_2y_0)\\ &+\ 2^{3 \times 8}\times (x_0y_3+x_1y_2+x_2y_1+x_3y_0)\\ &+\ 2^{4 \times 8}\times (x_1y_3+x_2y_2+x_3y_1)\\ &+\ 2^{5 \times 8}\times (x_2y_3+x_3y_2)\\ &+\ 2^{6 \times 8}\times (x_3y_3) \end{aligned} \] 因此，设\(\alpha\)为unit32_t类型数中只有低\(8\)位的任意数字，那么根据上述\(x\times y\)的拆分结果可以归结为 \[ \alpha \times \alpha, \alpha \times (\alpha << 8), \alpha \times (\alpha<<16),\alpha \times (\alpha<<24), \]

\[ (\alpha << 8)\times (\alpha<<24),(\alpha << 16)\times (\alpha<<24),(\alpha << 24)\times (\alpha<<24) \]

一共7种运算。每一种运算可以用一个乘法表表示，每个乘法表大小为\(2^8\times 2^8\times 4\ Bytes\).

以上为Galois field上的一些基本运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void galois_region_xor(char *r1,         /* Region 1 */
                       char *r2,         /* Region 2 */
                       char *r3,         /* Sum region (r3 = r1 ^ r2) */
                       int nbytes);      /* Number of bytes in region */

void galois_w08_region_multiply(char *region,       /* Region to multiply */
                                int multby,       /* Number to multiply by */
                                int nbytes,       /* Number of bytes in region */
                                char *r2,         
/* If r2 != NULL, products go here.Otherwise region is overwritten */
                                int add);         
/* If (r2 != NULL && add) the produce is XOR'd with r2 */

void galois_w16_region_multiply(char *region,       /* Region to multiply */
                                int multby,       /* Number to multiply by */
                                int nbytes,       /* Number of bytes in region */
                                char *r2,         
/* If r2 != NULL, products go here. Otherwise region is overwritten */
                                int add);         
/* If (r2 != NULL && add) the produce is XOR'd with r2 */

void galois_w32_region_multiply(char *region,       /* Region to multiply */
                                int multby,       /* Number to multiply by */
                                int nbytes,       /* Number of bytes in region */
                                char *r2,         
/* If r2 != NULL, products go here. Otherwise region is overwritten */
                                  int add);         
/* If (r2 != NULL && add) the produce is XOR'd with r2 */

// 上述三个函数均为将region中各个元素乘以multby
// 1. r2 == NULL,则将结果写入region，结束
// 2. r2 != NULL 且 add is false,则将结果写入r2
// 3. r2 != NULL 且 add is true,将结果与r2异或再写入r2

以上四个函数为域内乘法，第一个表示将两个等大的数组\(r_1\)和\(r_2\)按元素进行异或，将结果置入\(r_3\)中。后面3个函数主要用来求点积，具体的实现步骤已经标注在上面的注释中了，点积的概念将在之后介绍到。

（二）JErasure.c/JErasure.h

3.2.1 函数的参数介绍

在分析函数功能之前，先弄明白这两个文件中定义的函数的参数。

\(K\) = 数据块数量

\(M\) = 校验块(coding devices)数量

\(W\) = 字长

\(data\_ptrs[][]\) = 包含\(k\)个指向大小为size bytes的数据的指针的数组，即数据块指针，\(size\)必须是sizeof(long)的整数倍

\(coding\_ptrs[][]\) = 指向编码数据（大小为字节）的m个指针数组，即校验块指针

\(packetsize\) = 使用bitmatrix编码的编码块(coding block)大小

\(Matrix[]\) = 包含\(k\times m\)个整数(integer)的数组，即编码矩阵，其中\(i\)行\(j\)列元素为\(matrix[i\times k+j]\)

\(Bitmatrix[]\) = 包含\(kw \times mw\)个整数(integer)的数组，其中\(i\)行\(j\)列元素为\(bitmatrix[i\times kw+j]\)

\(Erasures[]\) = 已删除的设备(devices)(块)的\(id\)的数组，用于记录哪些块丢失 \(id∈[0, k+m-1]\) \(id∈[0, k-1]：数据块id\) \(id∈[k, k+m-1]：编码块(校验块)id\) \(例如：erasures[0] = 0;\) //第\(0\)个块丢失 \(erasures[1] = 3;\) //第\(3\)个块丢失 \(erasures[2] = -1;\) //结束标志

\(Operation[op][]\) = 包含5个整数的数组(五元组) \(4 : 进行操作 - 0表示复制，1表示异或\) \(0 : 源设备(device)[0,k+m-1](operation[op][0] = -1表示结束)\) \(1 : 源数据包(packet)[0,w-1]\) \(2 : 目标设备[0,k+m-1]\) \(3 : 目标数据包[0,w-1]\)

我这里只介绍各个接口的实现和作用，各位最好还是对照源码来理解各个参数的含义。

3.2.2 位矩阵编解码的时空优化方案

因为位矩阵的大小变成了\(kw\times mw\)，比之前的矩阵大了\(w^2-1\)倍，空间利用率极低。而且在编码校验块的时候，中间可能会有大量的XOR操作是重复的，例如 \[ P_{1,1}=D_{1,1} \otimes D_{1,2};\\ P_{1,2}=D_{1,1} \otimes D_{1,2} \otimes D_{2,2};\\ P_{2,1}=D_{1,1} \otimes D_{2,2} \otimes D_{3,1} \] 因此，可以由\[P_{1,2}=P_{1,1} \otimes D_{2,2} \\P_{2,1}=P_{1,2}\otimes D_{2,2}\otimes D_{3,1}\]来减少XOR次数，一般而言，\(kw\)和\(mw\)较大，所以以这种方式来减少XOR次数是可以减少编解码时间的。

刚刚那个栗子只减少了1次XOR操作，看起来8太行。现在来举个好一点的栗子： 由上面的图上所示，按照位矩阵的XOR操作得到校验块，可以得到： 但是很显然，中间有大量的XOR操作可以重复利用。如果将其重复的结果进行分类，则可以有以下结果： 很显然，这次是大大的减少所需的XOR操作。

以这种思路，JErasure库给出了两种方式来分别实现提高空间利用率和进一步减少XOR的操作数：

1
2
3
4
5
6
7
int **jerasure_dumb_bitmatrix_to_schedule(int k, int m, int w, int *bitmatrix);
//将bitmatrix转换为一系列操作。简单粗暴。
//返回一个operations[][]数组，具体实现方式为：
//若bitmatrix[index] == 1，则计算得到当前bitmatrix位置对应的数据块位置，如果在该行是第一个bitmatrix[index] == 1，则置operation为0(copy)，否则为1(XOR)

int **jerasure_smart_bitmatrix_to_schedule(int k, int m, int w, int *bitmatrix);
// 采用与上一函数类似的方法，不过使用之前的结果来计算新的点积。

这两个函数都是将位矩阵(bitmatrix)转化为了调度(schedule)，既减少空间开销，也减少了XOR次数。 先来分析第一个函数：(dumb) 其实就是在模拟位矩阵与数据包的矩阵乘法过程。例如： 例如: \[C_{11}=D_{11} \otimes D_{21} \otimes D_{22} \otimes D_{33}\otimes D_{41} \otimes D_{42} \otimes D_{43} \otimes D_{52}\] \(jerasure\_dumb\_bitmatrix\_to\_schedule\)即模拟\(D_{11}, \cdots, D_{52}\)的操作，且每个operation元素对应了一个源块和目标块的位置，以及要进行的操作。 例如，\(D_{11}\)对应的源块即为\((1,1)\)，目标块\(C_{11}\)即为\((1,1)\)，因为\(D_{11}\)在第一个位置上，所以操作为复制(copy)，即为\((0)\)，因此，\(D_{11}\)对应的五元组为\((1,1,1,1,0)\). 再例如，\(D_{21}\)对应的源块即为\((2,1)\)，目标块\(C_{11}\)即为\((1,1)\)，因为\(D_{21}\)不在第一个位置上，也就是说之前已经开始计算异或结果了，所以此时操作为异或(XOR)，即为\((1)\)，代表XOR \(D_{21}\)，因此，\(D_{11}\)对应的五元组为\((2,1,1,1,1)\).

现在来分析第二个函数：(smart) 前面那个函数只是开胃菜，这个函数才是对位运算的大大优化。基本思路与上一函数类似，但是这个会使用之前计算过的XOR结果(点积)来编码新的校验块。 下面是这种中间结果复用的实现方式：

先定义一些记号，以便后续说明： \(\text{from[]含有r个元素，初始置-1}\)

\(\text{diff[]含r个元素}，\text{diff[i]表示Mi中1的数量}\)

\(\text{flink[]和 blink[]用于定位top，top用于找当前待计算的校验块}\)

\(\text{bestdiff记录当前最小的diff[i]的值}\)

\(\text{bestrow记录当前bestdiff对应的diff[i]的 i的值}\)

实现步骤： 假定\(M\)为\(bitmatrix\)，\(V\)为输入的数据块，\(U\)为生成的校验块，\(notdone\)代表待生成的校验块\(id\)的集合，初始为\(0\) ~ \(mw-1\)，则步骤如下:

1. 选择未计算的校验块的packet且diff[i]最小的 i，即找到i∈notdone且diff[i]最小
2. 若from[i] = -1, 则令operation[op]的元素为M[i, j] = 1的所有对应的数据块;
   若from[i] ≠ -1, 则令operation[op]的第一个元素为校验块from[i]，之后的元素为第from[i]行与i行相异的bitmatrix中的元素对应的数据块
3. 从notdone中删除i
4. 对于notdone中的任一元素j，计算第j行与第i行中相异的元素的数量c，令x = c + 1，若x < diff[j]，则diff[j] = x，from[j] = i

也就是说，在某一次计算中，如果\(from[i] != -1\)，则说明第\(i\)个校验块的计算中用前面的计算过的结果来计算第i个校验块比直接进行矩阵乘法用到的XOR数要少，如果\(from[i] == -1\)，则说明用前面的结果计算该校验块不如直接计算来的快，就直接从\(bitmatrix\)中进行异或运算。

效率分析： 例如，在解码过程中，要计算得到\(D_0\)和\(D_1\)，通过一般的矩阵乘法计算，一共需要124次XORs。但是，如果按照上述方案： 1. 找到含有最少的1的一行(记为第\(i\)行)，即计算\(D_{1,3}\)对应的一行，一共有8个1，因此共7次XORs。 2. 计算其他9行(记为第\(j\)行)与\(D_{1,3}\)对应的\(bitmatrix\)的行中相异元素的数量，如果第\(j\)行中1的数量小于刚才计算出的数量+1，说明由第\(j\)行计算块得到结果需要的XOR数量多于由第\(j\)行计算块得到结果需要的XOR数量，此时将\(from[j]\)置为\(i\)，即第\(j\)行的XOR数量由第\(i\)行的结果来得到比当前方法更快。 3. 重复之，直到计算得到了所有的块。 根据上述理论分析，可以得出以下计算步骤： 此时一共需要46次XORs操作。相比之前的124次XORs，这种方法得到了大幅优化。

3.2.3 无返回值(void)的函数

接下来是几个无返回值的函数，比较简单，所以拿出来放在一块儿分析了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void jerasure_do_parity(int k, char **data_ptrs, char *parity_ptr, int size);
// 由data_ptrs直接进行XOR操作生成校验块，结果放入parity_ptr中

void jerasure_matrix_encode(int k, int m, int w, int *matrix,
                          char **data_ptrs, char **coding_ptrs, int size);
// 按常规方式编码，w必须是8，16，32

void jerasure_bitmatrix_encode(int k, int m, int w, int *bitmatrix,
                            char **data_ptrs, char **coding_ptrs, int size, int packetsize);
// 按常规方式对位矩阵编码，w ∈ [1, 32] and w ∈ N*

void jerasure_schedule_encode(int k, int m, int w, int **schedule,
                                  char **data_ptrs, char **coding_ptrs, int size, int packetsize);
// 使用jerasure_smart_bitmatrix_to_schedule()或者jerasure_dumb_bitmatrix_to_schedule()进行编码，具体方案由schedule[][]确定

没有什么难懂的地方，我根据自己的理解加了两句注释，大家看看代码也很容易就看懂了。

3.2.4 返回整数(integer)的函数

这种返回整数的函数都是值返回\(0\)和\(-1\)的，返回\(0\)说明这个函数完整的进行了操作，返回成功的标志；返回\(-1\)说明参数有误，中途中断，返回失败的标志。

1
2
3
int jerasure_matrix_decode(int k, int m, int w, 
                          int *matrix, int row_k_ones, int *erasures,
                          char **data_ptrs, char **coding_ptrs, int size);

\(k\)表示数据块，\(m\)表示校验块，\(matrix\)表示生成矩阵，\(row\_k\_ones\)用于记录编码的第一行是否为全1，用于优化，\(data\_ptrs\)表示指向数据块的指针，\(coding\_ptrs\)表示指向校验块的指针，\(erasures\)记录哪些块失效，\(size\)表示块大小。 这个函数表示创建\(GF(2^w)\)上的解码矩阵进行解码，且最终会丢弃解码矩阵。

1
2
3
int jerasure_bitmatrix_decode(int k, int m, int w, 
                            int *bitmatrix, int row_k_ones, int *erasures,
                            char **data_ptrs, char **coding_ptrs, int size, int packetsize);

表示创建\(GF(2)\)上的矩阵（位矩阵）进行解码，参数同上。\(packetsize\)是使用位矩阵进行编解码时一个\(packet\)的大小。

1
2
int jerasure_schedule_decode_lazy(int k, int m, int w, int *bitmatrix, int *erasures,
                            char **data_ptrs, char **coding_ptrs, int size, int packetsize, int smart);

若\(smart == 1\)，则采用\(jerasure\_smart\_bitmatrix\_to\_schedule()\)来创建调度（schedule），否则采用\(jerasure\_smart\_bitmatrix\_to\_schedule()\)。

1
2
int jerasure_make_decoding_matrix(int k, int m, int w, int *matrix, int *erased, 
                                  int *decoding_matrix, int *dm_ids);

创建解码矩阵，但是不解码，解码矩阵存放在\(decoding\_matrix\)中，\(dm\_ids\)含有\(k\)个整数，即用这\(k\)个存活块来构建解码矩阵，最终生成的\(decoding\_matrix\)含有\(k\times k\)个整数。

1
2
int jerasure_make_decoding_bitmatrix(int k, int m, int w, int *matrix, int *erased, 
                                  int *decoding_matrix, int *dm_ids);

同上，创建解码位矩阵，但是不解码，解码矩阵存放在\(decoding\_matrix\)中，\(dm\_ids\)含有\(kw\)个整数，即用这\(kw\)个存活块来构建解码矩阵，最终生成的\(decoding\_matrix\)含有\(kw\times kw\)个整数。

1
int *jerasure_erasures_to_erased(int k, int m, int *erasures);

将\(erasures[]\)转换成\(erased[]\)返回，其中\(erased[]\)标识了哪些位置上的 \(packet\)不可用。例如\(erased[2] = 1\)说明第\(2\)个\(packet\)不可用（从第\(0\)个\(packet\)开始计数）。举个栗子： 若\[erasures[] = \{0,2,3\}\]则\[ erased[] = \{1,0,1,1\} \]

3.2.5 求点积（dot product）的函数

1
2
3
void jerasure_matrix_dotprod(int k, int w, int *matrix_row,
                          int *src_ids, int dest_id,
                          char **data_ptrs, char **coding_ptrs, int size);

简单来说，就是将生成矩阵（编码矩阵/解码矩阵）的一行元素与数据块/幸存块相乘（求点积）。

数据块/幸存块的id存放在\(src\_ids\)中，例如： dot_product \(D_{1,1}\)的id为\(0\)，\(D_{4,3}\)的id为\(12\)，\(C_{1,1}\)的id为\(16\)等。

*注意：此处为了简单起见，给出的例子全部是以\(1\)开始计算id的，而一般情况下，应该从\(0\)开始。例如将上述\(D_{1\to5}\)和\(C_{1\to2}\)换成\(D_{0\to4}\)和\(C_{0\to1}\)，则\(D_{0,0}\)的id是\(0\)，\(D_{4,3}\)的id是\(11\)等。

编码/解码生成的块的id存放在\(dest\_id\)中。若\(src\_ids = null\)，则说明是在编码过程中，直接利用\(data\_ptrs\)计算点积即可，若\(src\_ids\ne null\)，则说明是在解码过程中，则需要从\(data\_ptrs\)和\(coding\_ptrs\)中得到对应的数据块/幸存块再计算点积。

该函数的对乘法计算进行了稍微的优化工作。因为点击计算需要\(GF(2^w)\)的乘法和加法，所以它会首先计算\(matrix\)中为\(0\)或\(1\)对应的块，然后再计算其他块，以简化计算的复杂度。例如： \[ \begin{bmatrix} \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & 3 & 0 & 2 & 1 & 0 & 3 & 7 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix} \begin{bmatrix} D_1 \\[8pt] D_2 \\[8pt] D_3 \\[8pt] D_4 \\[8pt] D_5 \\[8pt] D_6 \\[8pt] D_7 \\[8pt] D_8 \end{bmatrix}= \begin{bmatrix} \cdots \\[8pt] \cdots \\[8pt] \cdots \\[8pt] C_i \\ \cdots \\[8pt] \cdots \\[8pt] \cdots \end{bmatrix} \]

一般情况下，计算得到\[C_i=1D_1\oplus 3D_2\oplus 0D_3\oplus 2D_4\oplus 1D_5\oplus 0D_6\oplus 3D_7\oplus 7D_8\]

该函数则先计算0和1对应的块，即\(D_1,D_3,D_5,D_6\)。\(D_3,D_6\)对应的矩阵元素为0，所以可以忽略(\(\alpha \oplus 0=\alpha\))，即先得到\(D_1\oplus D_5\)。接下来再利用\(\text{galois\_w\_region\_multiply}\)计算剩余的非\(1\)的点积，然后将二者异或即得到\(C_i\)。

1
2
3
void jerasure_bitmatrix_dotprod(int k, int w, int *bitmatrix_row,
                             int *src_ids, int dest_id,
                             char **data_ptrs, char **coding_ptrs, int size, int packetsize);

含义同上一函数，方法为直接计算。从这里也可看出，\(GF(2)\)上的点积计算比\(GF(2^w)\)方便得多。

3.2.6 矩阵转置操作函数

1
int jerasure_invert_matrix(int *mat, int *inv, int rows, int w);

利用初等变换法求\(mat\)的逆矩阵，将结果放入\(inv\)中。大小为\(rows\times rows\)。

1
int jerasure_invert_bitmatrix(int *mat, int *inv, int rows);

利用初等变换法求\(mat\)的逆矩阵，将结果放入\(inv\)中。大小为\(rows\times rows\)。此时的\(w=1\)，因此也可以用\(jerasure\_invert\_matrix\)求逆，但是该函数的时间复杂度为\(O(n^2)\)，用上一函数令\(w=1\)的时间复杂度为\(O(n^3)\)。

1
int jerasure_invertible_matrix(int *mat, int rows, int w);

判断\(mat\)是否可逆，不会求逆。

1
int jerasure_invertible_bitmatrix(int *mat, int rows);

同上，判断\(mat\)是否可逆，不会求逆。

3.2.7 一些基本的矩阵操作函数

1
void jerasure_print_matrix(int *matrix, int rows, int cols, int w);

输出\(matrix\)，根据\(w\)的大小确定列间距。

1
void jerasure_print_bitmatrix(int *matrix, int rows, int cols, int w);

输出\(matrix\)，每\(w\)个字符后插入一个空格，每\(w\)行后插入一个空白行。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void jerasure_print_matrix(int *m, int rows, int cols, int w)
{
    int i, j;
    int fw;
    char s[30];
    unsigned int w2;

    if (w == 32)
    {
        fw = 10;
    }
    else
    {
        w2 = (1 << w);
        sprintf(s, "%u", w2 - 1);
        fw = strlen(s);
    }

    for (i = 0; i < rows; i++)
    {
        for (j = 0; j < cols; j++)
        {
            if (j != 0)
                printf(" ");
            printf("%*u", fw, m[i * cols + j]);
        }
        printf("\n");
    }
}

void jerasure_print_bitmatrix(int *m, int rows, int cols, int w)
{
    int i, j;

    for (i = 0; i < rows; i++)
    {
        if (i != 0 && i % w == 0)
            printf("\n");
        for (j = 0; j < cols; j++)
        {
            if (j != 0 && j % w == 0)
                printf(" ");
            printf("%d", m[i * cols + j]);
        }
        printf("\n");
    }
}

int main()
{
    int mat[] = {1, 5, 2, 7, 4, 
    			 5, 1, 3, 4, 7};
    int bitmat[6*15] = {   1, 0, 0,    1, 1, 0,    0, 0, 1,    1, 1, 1,    0, 1, 0,
                           0, 1, 0,    0, 0, 1,    1, 0, 1,    1, 0, 0,    0, 1, 1,
                           0, 0, 1,    1, 0, 0,    0, 1, 0,    1, 1, 0,    1, 0, 1,
                           
                           1, 1, 0,    1, 0, 0,    1, 0, 1,    0, 1, 0,    1, 1, 1,
                           0, 0, 1,    0, 1, 0,    1, 1, 1,    0, 1, 1,    1, 0, 0,
                           1, 0, 0,    0, 0, 1,    0, 1, 1,    1, 0, 1,    1, 1, 0};
    jerasure_print_matrix(mat, 2, 5, 3);
    putchar(10);
    jerasure_print_bitmatrix(bitmat, 2*3, 5*3, 3);
    system("pause");
    return 0;
}

输出结果为： 输出结果 

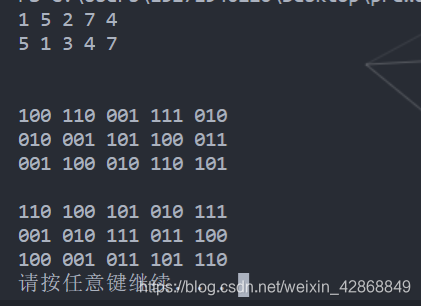
1
int *jerasure_matrix_multiply(int *m1, int *m2, int r1, int c1, int r2, int c2, int w);
计算矩阵乘法。\(m_1\)为\(r_1\times c_1\)，\(m_2\)为\(r_2\times c_2\)，计算\(m_1\times m_2\)，显然\(c_1=r_2\)。

3.2.8 监测函数

为评估编解码性能，JErasure库提供了一个监测函数。

1
void jerasure_get_stats(double *fill_in);

fill_in是含有\(3\)个double类型的向量，分别评价三个指标，其含义分别为：

  1. 使用`galois_region_xor()进行了XOR运算的字节数；

  2. 使用galois_w08_region_multiply(), galois_w16_region_multiply() or galois_w32_region_multiply()来乘以常数的字节数，即\(\text{region}\)的长度；

  3. 使用\(\text{memcpy()}\)复制的字节数。

调用该函数之后，上述三个指标将会被清空。具体如下：

1
2
3
4
5
6
7
8
9
void jerasure_get_stats(double *fill_in)
{
  fill_in[0] = jerasure_total_xor_bytes;
  fill_in[1] = jerasure_total_gf_bytes;
  fill_in[2] = jerasure_total_memcpy_bytes;
  jerasure_total_xor_bytes = 0;
  jerasure_total_gf_bytes = 0;
  jerasure_total_memcpy_bytes = 0;
}
Buy me a coffee.